Assignment #1 - Ch2. Continuous Dynamics - Embedded Systems Design and Modeling / Spring 2025

Problems:

Q2.

Show that if a system $A^\mathbb{R} \rightarrow B^\mathbb{R}$ is strictly causal and memoryless, then its output is constant. Constant means that the output $(S(x))(t)$ at time ( t ) does not depend on ( t ).

Q3.

This exercise studies linearity.

Show that the helicopter model defined in Example 2.1 is linear if and only if the initial angular velocity $\dot{\theta}_{y}(0) = 0$
Show that the cascade of any two linear actors is linear.
Augment the definition of linearity so that it applies to actors with two input signals and one output signal. Show that the adder actor is linear.

Q4.

Consider the helicopter of Example 2.1, but with a slightly different definition of the input and output. Suppose that, as in the example, the input is $T_y: \mathbb{R} \rightarrow \mathbb{R}$ , as in the example, but the output is the position of the tail relative to the main rotor shaft. Specifically, let the ( x-y ) plane be the plane orthogonal to the rotor shaft, and let the position of the tail at time ( t ) be given by a tuple ( ((x(t), y(t))) ) Is this model LTI? Is it BIBO stable?

Q5:

Consider a rotating robot where you can control the angular velocity around a fixed axis.

Model this as a system where the input is angular velocity $\dot{\theta}$ and the output is angle $\theta$ Give your model as an equation relating the input and output as functions of time.
Is this model BIBO stable?
Design a proportional controller to set the robot onto a desired angle. That is, assume that the initial angle is $\theta(0)=0$ , and let the desired angle be $\psi(t)=au(t)$ where ( u ) is the unit step function. Find the actual angle as a function of time and the proportional controller feedback gain ( K ). What is your output at ( t=0 )? What does it approach as ( t ) gets large?

Q6:

A DC motor produces a torque that is proportional to the current through the windings of the motor. Neglecting friction, the net torque on the motor, therefore, is this torque minus the torque applied by whatever load is connected to the motor. Newton’s second law (the rotational version) gives

$k_{T}i(t)-x(t)=I\frac{d}{dt}\omega(t)$

where ( k_T ) is the motor torque constant, ( i(t) ) is the current at time ( t ), ( x(t) ) is the torque applied by the load at time ( t ), ( I ) is the moment of inertia of the motor, and $\omega(t)$ is the angular velocity of the motor.

Assuming the motor is initially at rest, rewrite (2.15) as an integral equation.
Assuming that both ( x ) and ( i ) are inputs and $\omega(t)$ is an output, construct an actor
In reality, the input to a DC motor is not a current, but is rather a voltage. If we assume that the inductance of the motor windings is negligible, then the relationship between voltage and current is given by

$v(t)=R_i(t)+k_b\omega(t)$

where ( R ) is the resistance of the motor windings and ( k_b ) is a constant called the motor back electromagnetic force constant. The second term appears because a rotating motor also functions as an electrical generator, where the voltage generated is proportional to the angular velocity.

Modify your actor model so that the inputs are ( v ) and ( x ) rather than ( i ) and ( x ).

Q7:

Using your favorite continuous-time modeling software (such as LabVIEW, Simulink, or Ptolemy II), construct a model of the helicopter control system shown in Figure 2.4. Choose some reasonable parameters and plot the actual angular velocity as a function of time, assuming that the desired angular veloc- ity is zero, $\psi(t)=0$ , and that the top-rotor torque is non-zero, $T_t(t)=bu(t)$ . Give your plot for several values of ( K ) and discuss how the behavior varies with ( K ).
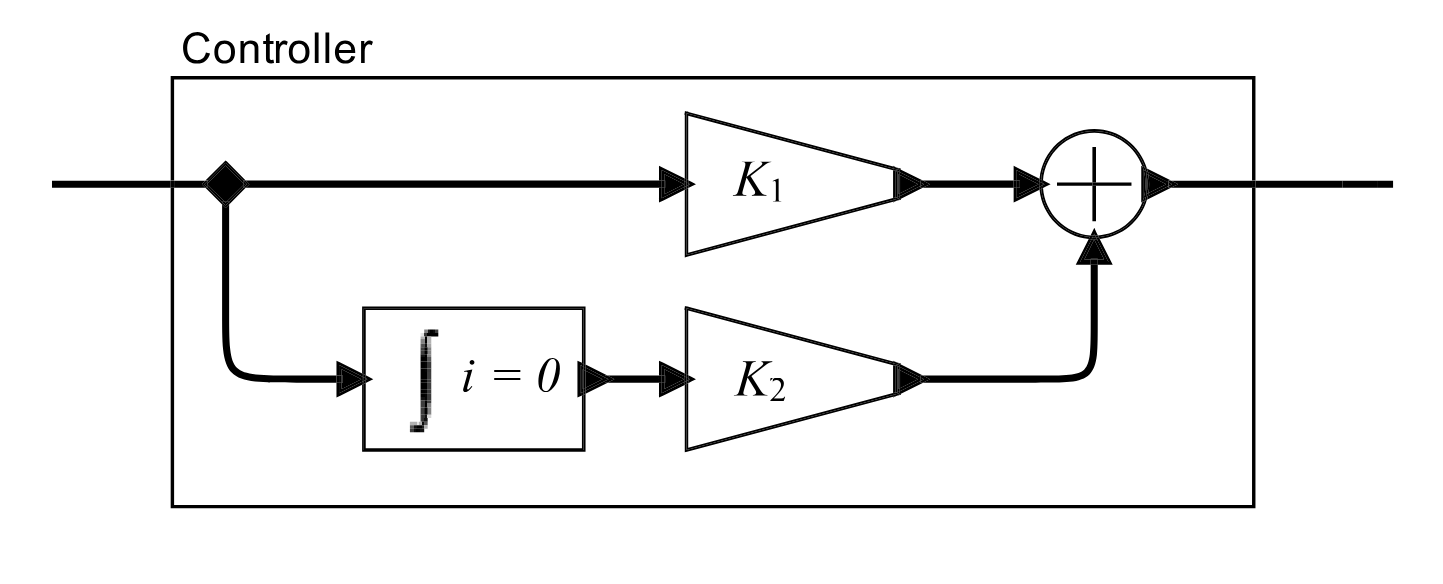
Modify the model of part 1 to replace the Controller of Figure 2.4 (the simple scale-by-(K) actor) with the alternative controller shown in Figure 2.6. This alternative controller is called a \textbf{proportional-integrator (PI) controller}. It has two parameter (K1) and (K2) . Experiment with the values of these parame- ters, give some plots of the behavior with the same inputs as in part 1, and discuss the behavior of this controller in contrast to the one of part 1.